Recently we have looked at the benefit of the Vol KO put for the investors. They indeed provide a cheap hedge, with a backtesting that is quite appealing. When products are so attractive for investors, it is generally because they exhibit complex risks for the banks.
Let us then explore the risks that banks take when selling Volatility KO puts.
As a reminder, the payout of a Put on S strike K, with a KO condition on volatility at Kσ, traded at time t and with maturity T is:
- Max ( K – S(T)/S(t), 0) if the realised volatility of S between t and T is below Kσ
- 0 otherwise
Strictly equivalently, it can be defined as
- Max ( K – S(T)/S(t), 0) if the realised variance of S between t and T is below Kσ2
- 0 otherwise
That last version can be useful when thinking of hedges as options on variance are more common than options on volatility.
To fix ideas, we will take the example of a strike of the Put at 100%, so K = 100%.
One can see quickly that there are two opposite effects in play in that product: a higher implied volatility means the Put will have more value, but the likelihood of a knock out is higher. To disentangle those effects, one can note that :
Vol Knock OUT Put = Vanilla Put – Vol Knock IN Put
For the bank, being short a Vol KO Put is equivalent to being short a Vanilla Put, easily hedgeable, and long a vol KI Put. We will now look at what being long a vol KI Put may mean.
One can look at the Vol KI put as a digital call on variance, the size of which is the value of the put. The value of the put is driven mainly by the spot level, and to a lesser extent by the vol. So we can plot the shape of the value the Vol KI Put as a function of volatility : when the implied variance is way below Kσ2, the vol KI put is almost. As the implied variance gets closer to Kσ2, the value starts increasing with the maximum acceleration around Kσ2. When the implied variance is much higher than Kσ2, the Vol KI Put behaves like a vanilla put and its sensitivity to vol is the same as a vanilla option.
Banks are then long vol convexity (long vol of variance) when the implied vol is below Kσ but become short gamma on variance when the implied vol goes above Kσ– cleary not a great position. That could be hedged (in theory only unfortunately…) by selling a tight call spread on variance and which size would be readjusted each time the spot moves. So ideally we would need our model able to tell us how variance moves with spot and how the skew of variance moves with spot.
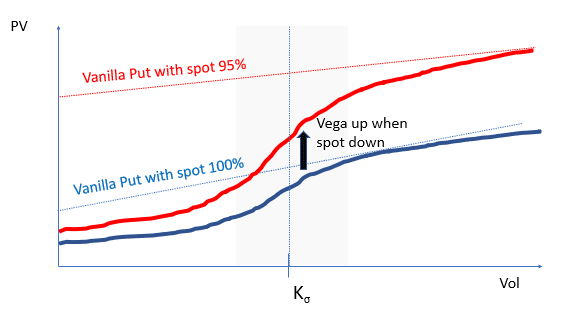
Value of the Vol KI Put as a function of implied vol, at a fixed level of spot.

When the spot moves, the size of the digital changes. We can plot the value of the Vol KI Put at two levels of spot. In red, the spot is at 95% of the initial value, so the put has more value than on the blue line, where the spot is at 100% of initial spot.
Value of the Vol KI Put as a function of implied vol at two levels of spot.

One can see clearly several phenomena from that graph.
First when the spot moves down (from blue curve to red curve), the slope of the curve increases, especially when the implied volatility is around the strike Kσ. so the bank gets longer vol (actually here longer variance) when the spot goes down. It is less true when the implied vol goes far above the strike Kσ.
The vega change with spot is the highest when implied vol is close to Kσ.
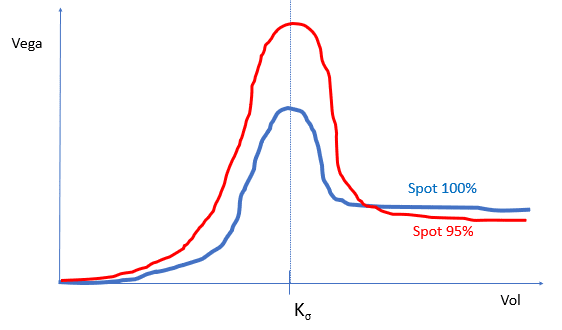
We can infer the shape of the vega (slope of the previous graph) at those two levels of spots:
Vega of the Vol KI Put at different spot levels
Conclusion:
When pricing and hedging a Vol KO Put, one ideally needs a model that can model correctly the way variance and volatility of variance move with spot, and that embed the skew of volatility of variance. That is particularly complex to achieve but unavoidable as those risks are at the very heart of the payout definition.
The day one vanilla hedge could be the buy of an ATM put and the sell of (many) downside puts.